Saat SMA, program linear menjadi salah satu bab yang sebenarnya mudah, namun malesin lantaran lama ngitungnya. Saya ingat betul ketika guru matematika wajib mengajar materi ini di kelas XI. Materi program linear nggak banyak hafalan rumus, hanya saja konsepnya terlalu njelimet serta dibutuhkan penalaran dalam memahami soal cerita. Makanya diperlukan waktu yang lama untuk mengerjakannya.
Program linear digunakan sebagai salah satu metode untuk memaksimalkan keuntungan toko atau kinerja perusahaan. Oleh karena itu, tak jarang materi ini muncul kembali di dunia perkuliahan. Ia akan bergabung dengan teori pengambilan keputusan lain biasanya dengan nama mata kuliah Riset Operasi. Meski ditempatkan berbeda tempat dengan kalkulus, tempat trigonometri dan logaritma berada, namanya matematika ya tetaplah matematika. Program linear selalu saja sulit dinalar.
Berikut soal program linear yang digunakan dalam Ujian Nasional Matematika IPA tahun 2018. Itung-itung bernostalgia jaman-jaman ketika UN masih menjadi momok menakutkan bagi siswa.
Seorang petani memiliki lahan pertanian seluas 8 hektar. Ia akan menanami lahan tersebut dengan tanaman padi dan jagung. Dari satu hektar tanaman padi dapat dipanen 3 ton padi, sedangkan dari satu hektar tanaman jagung dapat dipanen 4 ton jagung. Petani itu ingin memperoleh hasil panen tidak kurang dari 30 ton. Jika biaya menanam 1 hektar tanaman padi adalah Rp500.000,00 dan biaya menanam satu hektar tanaman jagung adalah Rp600.000,00, maka biaya minimum yang harus dikeluarkan petani adalah…
Nah, ceritanya ada petani yang pengin meminimalkan modalnya, nih. Dengan modal yang minimal, maka keuntungan yang akan didapatkan petani tersebut akan maksimal. Langkah pertama yang harus dilakukan tentu saja membuat model matematika terlebih dahulu. Mari kita modelkan per kalimat.
Seorang petani memiliki lahan pertanian seluas 8 hektar. Ia akan menanami lahan tersebut dengan tanaman padi dan jagung.
Ini artinya, dari 8 hektar tersebut akan dibagi menjadi beberapa hektar untuk menanam padi, serta beberapa hektar untuk menanam jagung. Misalkan x adalah luas lahan yang ditanami padi dan y adalah luas lahan yang ditanami jagung, model matematikanya sebagai berikut:
x + y ≤ 8
Kenapa tandanya kurang dari sama dengan (≤), bukan sama dengan (=)? Tentunya sang petani ingin sekali menggunakan semua lahannya sebanyak 8 hektar, namun kondisi tersebut bisa saja tidak dapat dilakukan karena kondisi yang lain. Oleh karena itu, dalam pemodelan masih dimungkinkan menggunakan lahan kurang dari 8 hektar, dengan sisa lahannya bisa saja kosong. Kenapa tandanya bukan lebih dari (>)? Ya gimana lagi, Bos. Si petani cuma punya lahan 8 hektar, memang kamu mau ngasih lebihannya? Lanjut ke kalimat berikutnya.
Dari satu hektar tanaman padi dapat dipanen 3 ton padi, sedangkan dari satu hektar tanaman jagung dapat dipanen 4 ton jagung. Petani itu ingin memperoleh hasil panen tidak kurang dari 30 ton.
Pada kalimat yang pertama tadi, kita sudah memisalkan x sebagai luas lahan padi dan y sebagai luas lahan jagung. Dengan memanfaatkan luas lahan yang tersedia, petani ingin menghasilkan panen yang tidak kurang dari 30 ton. Model matematikanya sebagai berikut.
3x + 4y ≥ 30
Setelah didapatkan kedua pertidaksamaan, ingat bahwa luas lahan baik yang digunakan untuk menanam padi maupun jagung selalu bernilai positif dimulai dari nol. Oleh karena itu, ditambahkan pertidaksamaan berikut:
x ≥ 0
y ≥ 0
Keempat pertidaksamaan tersebut sering disebut dengan fungsi kendala (constraint). Selain fungsi kendala, terdapat pula fungsi tujuan (objective). Untuk memahami fungsi tujuan, kita dapat memodelkan kalimat terakhir dari soal sebagai berikut:
Jika biaya menanam 1 hektar tanaman padi adalah Rp500.000,00 dan biaya menanam satu hektar tanaman jagung adalah Rp600.000,00, maka biaya minimum yang harus dikeluarkan petani adalah…
Dengan pemisalan x dan y yang telah diciptakan, maka model matematika dari fungsi tujuan soal tersebut adalah sebagai berikut:
f(x,y) = 500.000x + 600.000y
Tujuan yang ingin kita capai dalam permasalahan ini adalah meminimalkan fungsi f(x,y). Langkah selanjutnya adalah menggambarkan fungsi kendala ke dalam suatu bidang Cartesius. Cara ini disebut dengan cara grafik yang digunakan sebagai kurikulum pada jenjang SMA. Saat di perguruan tinggi, terdapat cara lain untuk menyelesaikan masalah program linear, yakni di antaranya metode simpleks.

Jika dicari irisan (perpotongan) kedua grafik dari fungsi kendala tersebut, maka akan dihasilkan grafik sebagai berikut:

Dari grafik tersebut, dapat terlihat tiga titik yang menjadi sudut dari daerah arsiran. Dari titik A(0,8), B(0,15/2) dan titik C yang belum diketahui. Sebelum memasukkan nilai-nilai titik ke dalam fungsi tujuan, kita harus melengkapi x dan y pada titik C, yakni dengan cara SPLDV. Kalau ini, sih, flashback ke pelajaran SMP saja ya, pasti semua juga pada hafal. Kalau-kalau bingung, perlu diragukan, nih, kelulusannya dari jenjang SMP. Ehehehe, canda. Pengerjaannya sebagai berikut:
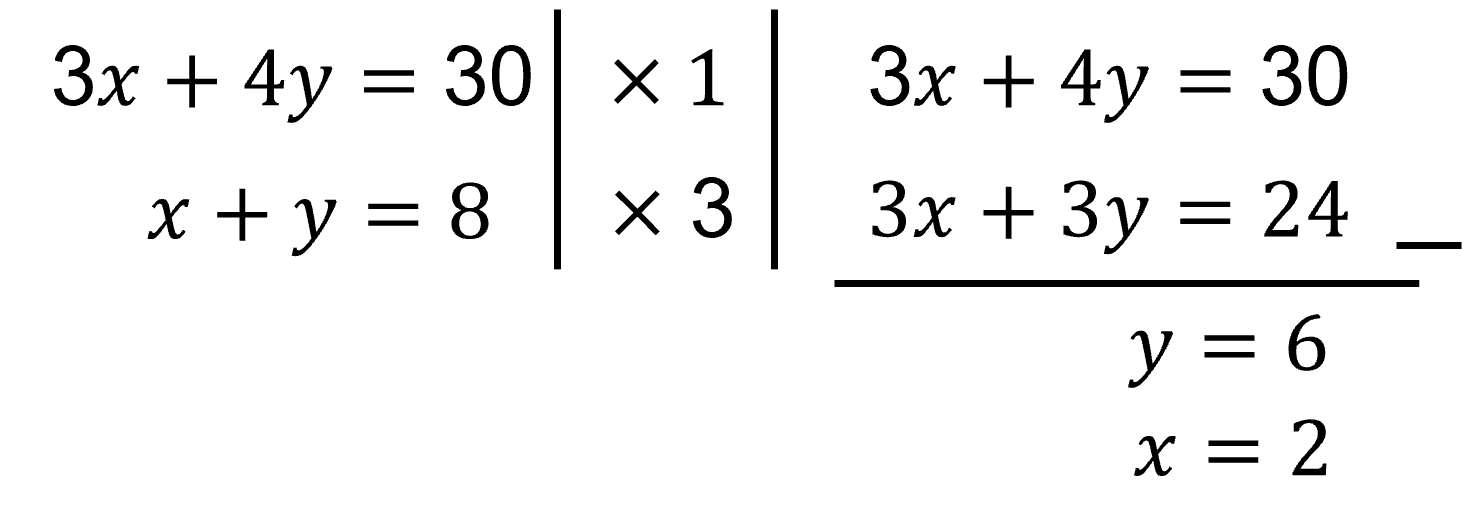
Setelah ketemu semua titik-titiknya, baru kita masukkan x dan y ke fungsi tujuan f(x,y) = 500.000x + 600.000y untuk mengetahui titik mana yang menghasilkan nilai minimum.
Untuk A(0,8), f(0,8) = 500.000(0) + 600.000(8) = Rp4.800.000
Untuk B(0,15/2), f(0,15/2) = 500.000(0) + 600.000(15/2) = Rp4.500.000
Untuk C(2,6), f(2,6) = 500.000(2) + 600.000(6) = Rp4.600.000
Jadi, jawabannya adalah 4.500.000, yakni nilai minimum yang dikeluarkan petani untuk menanam benih jagung dan benih padi, dengan rincian 0 hektar untuk benih padi dan 7.5 hektar untuk benih jagung. Pada soal ini terlihat bahwa penanaman jagung lebih menguntungkan dibandingkan padi.
Nah, begitulah salah satu contoh soal pembahasan mengenai program linear. Pembahasan soal matematika lain dapat disimak di lain hari, ya. Pusing, Gan!
BACA JUGA Menghitung Perbandingan Umur, Soal Langganan di Ujian Matematika dan tulisan Rezky Yayang Yakhamid lainnya.