Gugurnya Pak Tua menjadikan episode keenam (gganbu) paling memorable sepanjang series Squid Game. Selain itu, dalam episode Squid Game ini juga menunjukkan semua sifat kejahatan manusia yang sebenarnya serta naluri untuk bertahan hidup meskipun lawannya adalah kawannya sendiri. Permainan yang dimainkan sederhana, yakni kelereng, di mana pasangan pemain dapat dengan bebas menentukan permainannya sendiri.
Setiap pemain awalnya diberikan modal masing-masing 10 kelereng dan diberikan waktu 30 menit untuk bermain melawan pasangannya tanpa kekerasan. Pemain yang berhasil mendapatkan kesepuluh kelereng lawannya dinyatakan menang dan dapat melanjutkan ke permainan berikutnya.
Pada tulisan lama, saya telah menghitung peluang Nobita mendapatkan nilai nol hingga menghitung peluang memenangkan UNO. Saya akan bermain kembali dengan peluang untuk menghitung permainan kelereng ganjil-genap.
Permainan ini paling banyak dimainkan oleh pasangan pemain dalam episode gganbu Squid Game. Ganjil-genap dimainkan Gi-hun (tokoh utama) dengan Pak Tua (Il Nam Son), Sang-woo (pengusaha) dengan Ali (pekerja), dan Deok-su (preman) dengan pemain 278 (anteknya).
Peraturan permainan ini sederhana. Pemain lawan (Pak Tua, misalnya) hanya perlu menebak dengan benar ganjil atau genapkah jumlah kelereng yang ada pada genggaman lawannya (Gi-hun, misalnya). Pak Tua menaruh taruhan dalam genggamannya, di mana Gi-hun akan membayar sebanyak jumlah taruhannya apabila Pak Tua berhasil menebak dengan benar. Sebaliknya, taruhan milik Pak Tua akan diambil oleh Gi-hun apabila Pak Tua salah menebak.
Berapa peluang benar dan berapa peluang salah dalam menebak pada awal permainan?
Sebelum menghitung yang susah, kalanya kita dapat menghitung yang mudah terlebih dahulu, sekalian untuk mengingat konsep-konsep yang ada dalam peluang.
Pertama, semesta. Pada awal permainan ini, semesta kejadian S={1,2,3,4,5,6,7,8,9,10} karena setiap pemain dimodali 10 butir kelereng.
Kedua, kejadian. Kejadian ganjil adalah Ganjil={1,3,5,7,9} sedangkan kejadian genap adalah Genap={2,4,6,8,10}.
Maka, jika kita rangkum pada awal permainan, n(S)=10, n(Ganjil)=5, dan n(Genap)=5. Dengan begitu, peluang kelereng dalam genggaman adalah ganjil adalah P(Ga)=n(Ga)/n(S) = 5/10 = 0,5. Begitu pula sebaliknya.
Dalam episode keenam Squid Game tersebut, Son-woo tidak percaya kepada Ali dan mengatakan: “Bagaimana kau bisa terus memenangkannya? Peluang permainan ini 50:50.” Apakah peluangnya akan tetap 50:50 selama permainan? Tentu saja tidak, permainan berjalan dinamis dan peluang akan dipengaruhi oleh jumlah kelereng lawannya.
Berapa peluang benar dalam menebak jika jumlah kelerengnya sudah berkurang/bertambah?
Misalkan gim pertama di Squid Game Son-woo melawan Ali telah dimainkan dengan taruhan satu butir kelereng dan dimenangkan oleh Ali. Pada gim kedua, kelereng Ali berjumlah 11 dan Sun-woo berjumlah 9. Berikut ilustrasi kelereng Sun-woo.
Ganjil = {1,3,5,7,9}
Genap = {2,4,6,8}
S = {1,2,3,4,5,6,7,8,9}
Misalkan penebak kedua adalah Ali, maka peluang kelereng Sun-woo adalah ganjil adalah n(Gaanjil)/n(S) = 5/9 = 55,56% sedangkan peluang kelereng Sun-woo adalah genap adalah n(Genap)/n(S) = 4/9 = 44,44%. Jadi, pada gim kedua, apakah yang harus ditebak Ali? Tentu saja yang peluangnya lebih besar, yakni ganjil.
Bagaimana tips memenangkan permainan dengan mengetahui peluangnya?
Dari ilustrasi sebelumnya dapat disimpulkan, ketika jumlah kelereng lawan adalah ganjil, maka peluang kelereng dalam genggaman adalah ganjil selalu lebih besar dari peluang genap. Sedangkan, apabila jumlah kelereng lawan genap, maka peluang kelereng yang digenggam genap atau ganjil sama saja 50:50. Sebagai simulasi, saya mencoba menampilkan tabel berikut.
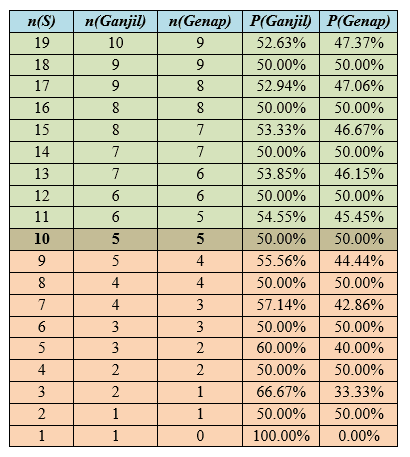
Dari tabel tersebut juga terlihat bahwa semakin sedikit jumlah kelereng modal, maka akan semakin besar peluang untuk menggenggam jumlah ganjil.
Pada permainan pertama, jika kita menjadi penebak pertama, taruhlah taruhan kelereng ganjil agar baik penebak maupun penggenggam memiliki kelereng ganjil dan dapat dipermainkan peluangnya. Berharaplah agar menang sehingga jumlah kelereng lawan menjadi lebih sedikit dari 10 sehingga peluangnya lebih besar.
Pada permainan kedua dan seterusnya, jika kita sebagai penebak, tentu haruslah menebak ganjil saat seluruh kelereng lawan berjumlah ganjil karena peluangnya akan lebih besar. Kemudian, taruhlah taruhan berjumlah genap agar mempertahankan kondisi ganjil.
Oh, ya. Aturlah taruhan agar jumlah kelereng lawan pada akhirnya adalah 1 karena sudah pasti jawaban ganjil akan benar. Kemudian, apabila kita sebagai penggenggam, genggamlah kelereng berjumlah genap karena lawan yang “jago matematika” pasti akan mengira peluang ganjil lebih besar.
Bagaimana peluang memenangkan seluruh permainan kelereng ganjil-genap?
Misalnya, Ali menjalankan rencana sesuai tips matematis sebelumnya. Jika Ali menaruh taruhan 1 kelereng pada gim pertama, dan 2 kelereng pada gim selanjutnya, peluang kemenangan Ali apabila pada keseluruhan permainan Ali selalu menjadi penebak adalah sebagai berikut.
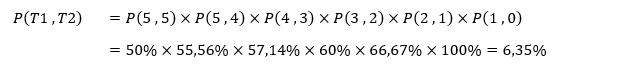
Perhitungan tersebut disimulasikan dalam tabel berikut.
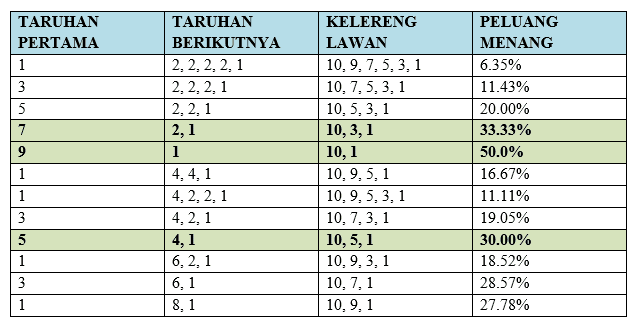
Pada tabel tersebut, peluang kemenangan tertinggi adalah pada taruhan (9, 1); (7, 2, 1); dan (5, 4, 1). Tapi jangan senang dulu. Taruhan yang besar tentu akan menjadikan risiko kekalahan yang besar pula. Saya akan mencoba menghitung peluang kekalahannya sebagai berikut.
Jika Ali menaruh taruhan 1 kelereng pada gim pertama, dan 2 kelereng pada gim selanjutnya, peluang kekalahan Ali apabila pada keseluruhan permainan Ali selalu menjadi penebak adalah sebagai berikut.
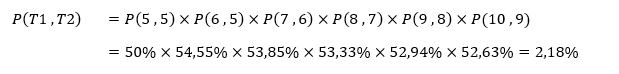
Perhitungan tersebut disimulasikan dalam tabel berikut.
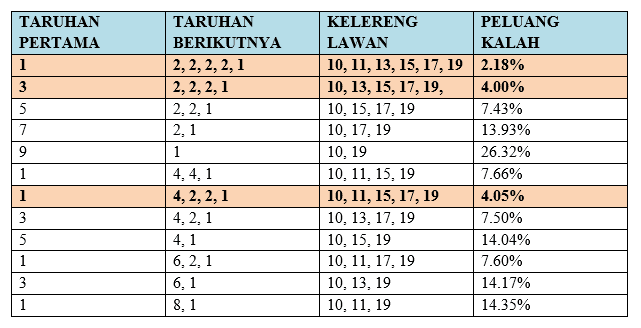
Pada tabel tersebut, peluang kekalahan terendah adalah pada taruhan (1, 2, 2, 2, 2, 1); (3, 2, 2, 2, 1); dan (1, 4, 2, 2, 1). Ingat, ancer-ancer tersebut tentu hanya berlaku jika dan hanya jika kita selalu di posisi penebak dan lawan di posisi penggenggam.
Apabila permainan berjalan dinamis dengan penebak dan penggenggam dilakukan secara bergantian, dapat dilakukan perhitungan sendiri sesuai pada rumus awal yakni jumlah kejadian ganjil n(Ganjil) dibagi jumlah semesta kejadian n(S), yakni sebanyak jumlah kelereng lawan. Berikut formula untuk menghitung peluang suatu kejadian A.
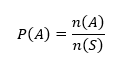
Saya ingat, pada scene memilih pasangan, terdapat guru matematika yang mengajak Gi-hun untuk bermain bersama, tapi Gi-hun menolaknya dan lebih memilih bermain bersama Pak Tua.
Pada permainan berikutnya, guru matematika tersebut terlihat masih hidup dan menghitung peluang pada permainan jembatan kematian. Mungkin saja si guru Matematika tersebut memanfaatkan kepandaiannya dalam ilmu peluang tersebut dalam permainan kelereng, kan?


















