Ada bermacam teori konspirasi di sekitar anime satu ini. Salah satu yang paling kejam, konon tokoh Nobita diangkat dari kisah nyata seorang pasien skizofrenia dan Doraemon hanya imajinasi Nobita. Tapi di sini yang mau saya soroti adalah teori konspirasi yang menyatakan Nobita tidak benar-benar bodoh. Saya akan menganalisis teori konspirasi ini dengan menggunakan teori Peluang, salah satu mata kuliah statistika yang pernah saya pelajari dengan bobot 3 SKS.
Seperti yang kita tahu, dalam cerita-ceritanya Nobita adalah karakter yang digambarkan Fujiko Fujio sebagai siswa SD yang pemalas dan bodoh. Saking bodohnya, hampir di setiap ulangannya dia selalu memperoleh nilai nol. Ya, nol bulat, bukan hasil pembulatan ke bawah. Hal tersebutlah yang membawa dirinya selalu dimarahi ibunya atau kalau beruntung dimarahi Doraemon saja. Atas kebodohannya, ia selalu menjadi bulan-bulanan Gian dan Suneo.
Nilai nol Nobita menjadi kekhawatiran saya. Memangnya semudah itu ya mendapat nilai nol di sekolah? Analisis ini berangkat dari akun Instagram @ngobrolmatematika yang beberapa hari lalu mengeluarkan analisis singkat dan konspiratif bahwa Nobita sebenarnya pintar. Saya akan melengkapi analisis dengan berbagai asumsi kenapa Nobita sampai mendapat nilai nol.
Mengapa Nobita selalu dapat nilai nol, asumsi #1 Ulangan Nobita berbentuk soal esai dan/atau isian singkat
Dalam bentuk soal semacam ini, semua kemungkinan nilai terbuka dari nol sampai 100 atau nilai sempurna. Umumnya bentuk soal esai diletakkan pada ujian-ujian yang sifatnya hapalan atau mengetes kemampuan berpendapat, seperti agama atau kewarganegaraan. Selain itu soal model ini juga dipakai mengetes kemampuan menulis siswa pada ujian bahasa.
Pada bentuk soal esai, penilaian bersifat subjektif. Nilainya pun bisa jadi berbeda antarguru. Guru yang baik biasanya menghargai tulisan pada esai dengan memberikan upah tulis, ya tentunya jika siswa menulis. Pada kemungkinan ini kita bisa asumsikan guru Nobita baik, namun Nobita sengaja mengosongkan jawabannya. Bukan bodoh, dia hanya sedang merendah.
Kemungkinan lain adalah guru Nobita benar-benar guru yang kejam sehingga tidak memberikan nilai upah tulis sekalipun ada tulisan di kertas jawabannya. Sekeras apa pun dan sepanjang apa pun tulisan Nobita pada lembar esainya, tetap saja tidak akan membuahkan nilai. Saya rasa asumsi ini yang paling tepat. Walaupun Nobita pemalas, tapi tidak akan melakukan tindakan bodoh seperti mengosongkan lembar esainya.
Mengapa Nobita selalu dapat nilai nol, asumsi #2 Bentuk soal pilihan ganda tetapi Nobita mengosongkan lembar jawaban
Dengan bentuk soal mana pun, jika Nobita merendah terus dengan cara mengosongkan lembar jawabannya maka nilainya akan tetap nol bulat. Tentu dengan disertai berbagai asumsi lain seperti sistem skor 1-0-0 atau 4-0-1, tidak ada bonus soal atau tidak ada poin tambahan. Walau saya rasa asumsi ini tidak masuk akal, Nobita tidak akan secara sengaja tidak berusaha sama sekali.
Mengapa Nobita selalu dapat nilai nol, asumsi #3 Bentuk soal pilihan ganda, sistem skor 4-0-1, dan Nobita menjawab acak
Dalam sistem ini, siswa yang menjawab—memilih opsi—benar akan diberi nilai 4, jika jawaban kosong (tidak memilih) maka diberi nilai 0, dan jika memilih opsi dengan salah akan diberi pengurangan nilai sebesar 1 poin. Maka dari itu biasanya di sistem seperti ini siswa cenderung tidak menjawab jika tidak tahu.
Soal pilihan ganda dengan sistem skor 4-0-1 memang jarang digunakan pada soal-soal ujian biasa setingkat SD bahkan hingga SMA. Biasanya sistem skor 4-0-1 diterapkan pada soal-soal olimpiade—OSN, OSK, dan semacamnya, atau soal seleksi masuk PTN—seperti perhitungan skor SBMPTN tahun 2017 ke belakang. Namun, kita akan tetap menggunakan asumsi sistem skor 4-0-1 dengan alasan sistem pendidikan di Jepang lebih maju dari Indonesia.
Asumsi ini bisa dijelaskan dengan teori peluang dan sedikit statistika. Pada umumnya di soal pilihan ganda terdapat 5 opsi jawaban: A, B, C, D, dan E. Akan ada 1 jawaban benar dan 4 jawaban salah. Maka peluang untuk menjawab benar adalah 1/5 = 0,2 sedangkan peluang untuk menjawab salah adalah 2/5 = 0,8.
Sekarang kita gunakan konsep nilai harapan (expected value). Asumsikan Nobita menjawabnya dengan acak karena semalaman berpetualang ke Negeri Awan. Jika menggunakan konsep frekuensi harapan, dari 50 soal yang dikerjakan Nobita dengan sistem skor 4-0-1, maka akan didapat nilai harapan Nobita sebagai berikut:
Nilai = (peluang benar x jumlah soal x nilai benar) + (peluang salah x jumlah soal x nilai salah)
Nilai = (0,2 x 50 x 4) + (0,8 x 50 x -1) = 40 + (-40) = 0
Saya sedikit mempercayai asumsi ini karena Nobita telah berusaha walaupun menjawabnya dengan acak. Namun, masih ada ganjalan besar di benak saya apakah mungkin siswa SD di Jepang sudah sangat canggih sehingga sudah diberi sistem skor seperti mahasiswa di Indonesia. Agaknya tidak terlalu lazim. Jadi bagaimana jika ternyata sistem skornya 1-0-0?
Mengapa Nobita selalu dapat nilai nol, asumsi #4 Bentuk soal pilihan ganda, sistem skor 1-0-0, dan Nobita tahu jawaban benarnya
Sistem skor pilihan ganda yang banyak dipakai saat ini adalah 1-0-0, di mana siswa hanya memperoleh poin ketika menjawab benar dan tidak memperoleh poin juga tidak mendapat pengurangan poin jika memilih opsi yang salah atau mengosongi opsi jawaban. Sistem ini dipakai di segala lini ujian formal yang mengukur kemampuan, seperti ulangan harian, ujian tengah dan akhir semester, Ujian Sekolah (US), sampai Ujian Nasional a.k.a. UN yang saat ini sudah dihapuskan.
Sama seperti sebelumnya, kita berasumsi terlebih dahulu bahwa Nobita tidak belajar dan menjawab acak. Soal terdiri dari 5 opsi jawaban dengan 1 jawaban benar dan 4 jawaban salah. Maka peluang menjawab benar untuk satu soal adalah 0,2 sedangkan peluang menjawab salah untuk satu soal adalah 0,8.
Pertama, kita mencoba memakai pendekatan nilai harapan (expected value). Misal jumlah soal yang dikerjakan adalah 50 soal dan Nobita mengerjakan semuanya secara acak. Maka harapan nilainya adalah sebagai berikut:
Nilai = (peluang benar x jumlah soal x nilai benar) + (peluang salah x jumlah soal x nilai salah)
Nilai = (0,2 x 50 x 1) + (0,8 x 50 x 0) = 10 + 0 = 10 dari 50 poin = 20 dari 100 poin
Kedua, kita mencoba menghitung dengan memakai pendekatan peluang kejadian bersyarat. Rumus umumnya adalah
P(A ∩ B) = P(A) x P(B|A)
Maksudnya peluang A dan B adalah peluang terjadinya A dikalikan dengan peluang terjadinya B dengan syarat A terjadi. Kita berasumsi soal-soal tersebut saling bebas (mutually exclusive), artinya soal nomor 2 tidak berkaitan dengan apa yang dilakukan pada soal nomor 1 dan seterusnya. Maka perhitungannya adalah:
P(Ai) = peluang salah menjawab soal ke i
P(A1 ∩ A2 ∩ … ∩ A50) = 0,8 x 0,8 x …. x 0,8 = (0,8)^50 = 1,4272 x 10^(-5) = 0,0014272%
Lihat, sedikit sekali kan peluang menjawab salah semua? Lantas bagaimana peluang orang-orang yang mendapat poin sempurna seratus ketika menjawabnya dengan acak? Apakah kita bisa mendapat nilai 100 dengan keberuntungan semata? Kita lihat perhitungannya:
P(Bi) = peluang benar menjawab soal ke i
P(B1 ∩ B2 ∩ … ∩ B50) = 0,2 x 0,2 x …. x 0,2 = (0,2)^50 = 1,1258 x 10^(-35)
Wow, bayangkan, 35 nol di belakang koma. Susah pakai banget. Untuk mendapat nilai 100 kamu tidak dapat dengan asal menebak saja kecuali jika kamu ditakdirkan memiliki indra keenam yang baik. Jika dibuat tabel distribusi peluang binomial dengan
P(X=x) = nCx . p^x . (1-p)^(n-x)
akan menjadi sebagai berikut:
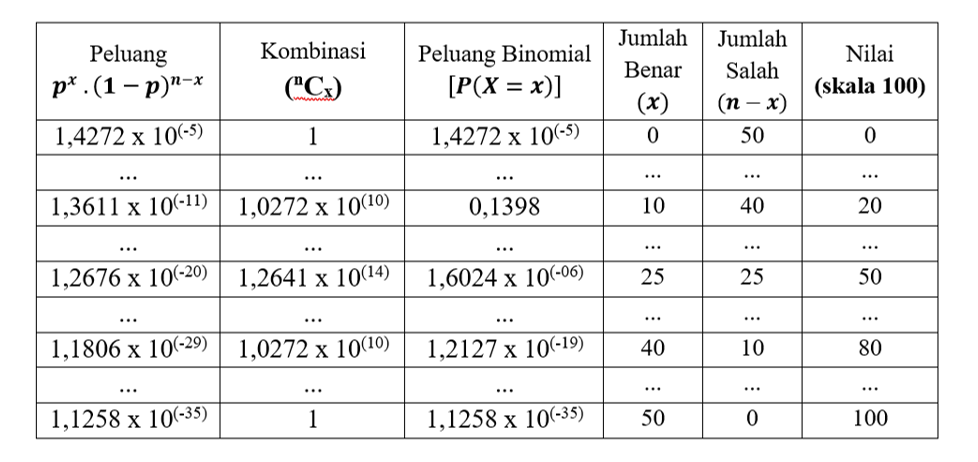
Berdasarkan aksioma probabilitas, nilai-nilai peluang diskrit jika ditambahkan semua akan bernilai 1 alias sebuah kepastian. Nilai-nilai peluang binomial tersebut jika dihitung semua dan dijumlahkan dari P(X=0) hingga P(X=50), akan bernilai 1.
Saya membuat dalam diagram garis agar terlihat jelas bentuk distribusinya–seharusnya dibuat dalam diagram batang. Berikut adalah diagramnya:
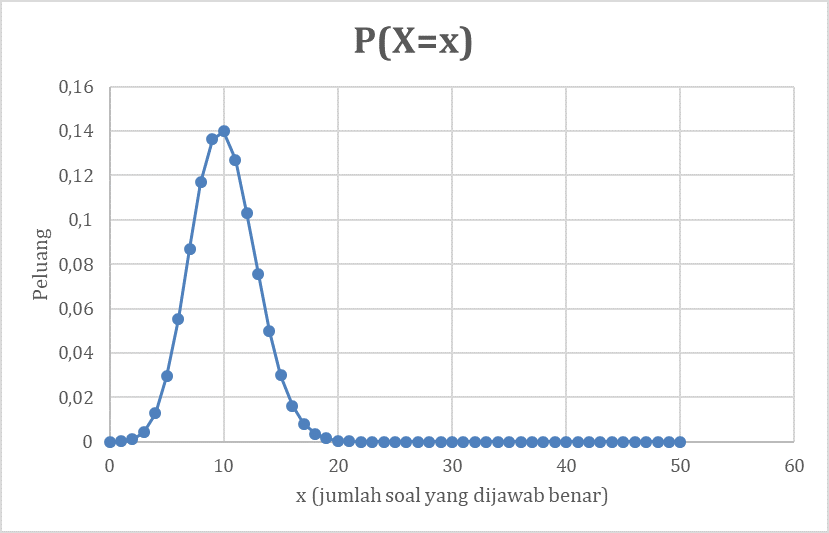
Maka terungkaplah, Nobita tidak mungkin mendapat nol bila ia menjawab soal dengan acak. Kemungkinan satu-satunya untuk bisa dapat nol bulat adalah: Nobita sendiri mengetahui salah satu dari keempat jawaban salahnya dan ia sengaja memilih opsi yang salah tersebut. Atau mungkin yang lebih tragis, Nobita sudah tahu semua jawaban benarnya dan di setiap soal yang ia lalui, ia selalu menghindari jawaban benar tersebut agar salah.
Namun, setelah tabel distribusi peluang di atas didapatkan, ada pelajaran yang dapat kita ambil, yakni ketika menjawab soal secara acak, untuk mendapat nilai nol saja peluangnya kecil, apalagi mendapat nilai seratus.
Saya jadi pusing.
Featured image: doraemon.fandom.com
BACA JUGA Analisis Statistik Tingkat Keambyaran Lagu-lagu Didi Kempot dan tulisan Rezky Yayang Yakhamid lainnya.
Terminal Mojok merupakan platform User Generated Content (UGC) untuk mewadahi jamaah mojokiyah menulis tentang apa pun. Submit esaimu secara mandiri lewat cara ini ya.
Pernah menulis di Terminal Mojok tapi belum gabung grup WhatsApp khusus penulis Terminal Mojok? Gabung dulu, yuk. Klik link-nya di sini.























